Sıralama Algoritmaları - 2. Büyük O Gösterimi

07.01.2014 5.592 0 Paylaş

Yazı dizisinin 2. bölümü

Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Daha açık şekilde anlatmak gerekirse, bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.

Bu gösterim ilk olarak Alman sayılar kuramcısı Paul Bachmann tarafından 1892 yılında yazdığı Analytische Zahlentheorie kitabında kullanılmıştır. Gösterim bir başka Alman matematikçi olan Edmund Landau tarafından yaygın kullanıma sokulmuştur, bundan ötürü bazen Landau sembolü olarak da anılır. Büyük O, İngiliz dilindeki "order of" yani bir şeyin derecesi anlamına gelen söz öbeğini hatırlatmak amacı ile kullanılıyordu ve ilk olarak büyük omicron harfi idi; günümüzde büyük O kullanılmakta ve 0 sayısı hiç kullanılmamaktadır.

Kullanım alanları

Bu gösterimin biçimsel olarak yakın ama temelde farklı iki kullanımı vardır: sonsuz asimptotikler ve infinitesimal asimptotikler. Bu ayrım sadece uygulamadadır ancak "büyük O"nun biçimsel tanımı her iki durumda aynı olup işlev argümanının limitleri değişmektedir.

Sonsuz asimptotikler

Büyük O gösterimi algoritma başarım çözümlemesinde faydalıdır. Söz gelimi n boyundaki bir problemi çözmek için gereken zaman (adım sayısı) T(n) = 4n² - 2n + 2 olarak bulunabilir.

n büyüdükçe n² terimi o kadar hızlı büyüyecektir ki diğer terimlerin büyüme hızı buna kıyasla ihmal edilebilir kadar düşük kalacaktır; örneğin n = 500 için 4n² terimi 2n teriminin 1000 katı büyüklüğünde olacaktır ve dolayısıyla bu ikinci terimin değeri tüm ifadenin değerini belirlemede çoğu amaç bakımından ihmal edilebilir bir etkiye sahip olacaktır.

Buna ek olarak, aynı ifadeyi n³ veya 2n terimleri içeren bir ifade ile kıyaslayacak olursak katsayılar da anlamlarını yitirecektir. T(n) = 1.000.000n² ve U(n) = n³ olsa bile ikinci ifade, n 1.000.000'u geçtikçe birinci ifadeye kıyasla daima daha büyük olacaktır (T(1.000.000) = 1.000.000³ = U(1.000.000)).

O halde Büyük O gösterimi işin özünü sade biçimde sunmaktadır: şu şekilde yazabilir

$T(n)\in O(n^2)$

ve algoritmanın n2 dereceden zaman karmaşıklığına sahip olduğunu söyleyebiliriz.

Sonsuz küçük asimptotikler

Büyük O aynı zamanda bir matematiksel işlev için geliştirilen yaklaşık işlevin hata terimini tarif etmek için de kullanılabilir. Örneğin, :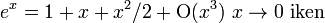 $e^x=1+x+x^2/2+\hbox{O}(x^3)\hbox{ } x \to 0 \hbox{ }\hbox{iken}$ ifadesi hatanın (yani ex - (1 +x + x2 / 2) farkının) mutlak değer bakımından, sıfıra yeterince yakın x değerleri için bir sabit çarpı x3değerinden daha küçük olduğunu belirtir.

Sık rastlanan işlev dereceleri

Aşağıda algoritma çözümlemesinde sıkça karşılaşılan işlev derecelerini görebilirsiniz. Tüm bunlar n sonsuza giderken durumunda belirtilmiştir. Daha yavaş büyüyen işlevler önce listelenmiştir. c keyfi bir sabit değerdir.

Gösterim	İsim
O(1)	sabit
O(log * n)	tekrarlı logaritmik
O(logn)	logaritmik
O([logn]c)	logaritmik çokterimli
o(n)	alt doğrusal
O(n)	doğrusal
O(nlogn)	doğrusal logaritmik (linearitmik), sözde doğrusal veya üst doğrusal
O(n2)	karesel
O(nc), c > 1	çokterimli, bazen "cebirsel" de denir
O(cn)	üssel, bazen "geometrik" de denir
O(n!)	faktöryel, bazen "kombinatoryel" de denir